Measuring changes in students' informal statistical reasoning skills through the ethno-flipped classroom model: Stacking and racking analysis
##plugins.themes.bootstrap3.article.main##
Abstract
Statistical reasoning is widely recognized as a fundamental skill for preparing students to navigate a data-driven global society. However, research on the development of informal statistical reasoning, particularly when facilitated through an ethno-flipped classroom model, remains limited. Furthermore, few studies employ longitudinal approaches, such as stacking and racking, to assess continuous changes in students' reasoning development over time. Most existing research relies on pre–post comparisons and lacks comprehensive analysis at both the person and item levels. This study investigates changes in students' informal statistical reasoning using the Partial Credit Rasch Model, incorporating stacking and racking analysis. A total of 152 twelfth-grade students participated in a 12-week ethno-flipped classroom intervention. The informal statistical reasoning test, consisting of five open-ended items, demonstrated sufficient validity for use in both the instructional intervention and the Rasch-based analysis. Item validity was assessed as a key parameter within the Rasch measurement framework. The findings revealed significant improvements in student proficiency and a decrease in item difficulty. Notably, 66 students reached Level 5, reflecting integrated process reasoning. These results support the effectiveness of the ethno-flipped classroom model in enhancing informal statistical reasoning. This study contributes to the design of contextual, adaptive instruction and offers a robust Rasch-based framework for monitoring reasoning development longitudinally.
##plugins.themes.bootstrap3.article.details##

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
The author is responsible for acquiring the permission(s) to reproduce any copyrighted figures, tables, data, or text that are being used in the submitted paper. Authors should note that text quotations of more than 250 words from a published or copyrighted work will require grant of permission from the original publisher to reprint. The written permission letter(s) must be submitted together with the manuscript.References
Abeysekera, L., & Dawson, P. (2015). Motivation and cognitive load in the flipped classroom: definition, rationale and a call for research. Higher Education Research & Development, 34(1), 1–14. https://doi.org/10.1080/07294360.2014.934336
Amin, N. F. M., Saud, M. S., Buntat, Y., & Latif, A. A. (2013). The application of rasch measurement model in measuring change in students self-directed learning readiness. Advanced Science Letters, 19(12), 3736–3738. https://doi.org/10.1166/asl.2013.5242
Andrade, M., & Coutinho, C. (2016). Implementing flipped classroom in blended learning environments: A proposal based on the cognitive flexibility theory. In E-learn: World conference on e-learning in corporate, government, healthcare, and higher education, (pp. 1115–1125). https://www.learntechlib.org/p/174050
Andrich, D. (2017). Advances in social measurement: A rasch measurement theory. In F. Guillemin, A. Leplege, S. Briancon, E. Spitz, & J. Coste (Eds.), Perceived health and adaptation in chronic disease (pp. 66–91). Routledge. https://doi.org/10.1201/9781315155074-7
Attard, C., & Holmes, K. (2020). An exploration of teacher and student perceptions of blended learning in four secondary mathematics classrooms. Mathematics Education Research Journal, 34(4), 719–740. https://doi.org/10.1007/s13394-020-00359-2
Bond, T., & Fox, C. M. (2015). Why Measurement Is Fundamental. In Applying the rasch model: Fundamental measurement in the human sciences (3rd ed.). Routledge. https://doi.org/10.4324/9781315814698
Bond, T., Yan, Z., & Heene, M. (2020). Applying the rasch model: Fundamental measurement in the human sciences (4th ed.). Routledge. https://doi.org/10.4324/9780429030499
Combrinck, C., Scherman, V., & Maree, D. (2016). Evaluating anchor items and reframing assessment results through a practical application of the rasch measurement model. South African Journal of Psychology, 47(3), 316–329. https://doi.org/10.1177/0081246316683569
Conway, B., Gary Martin, W., Strutchens, M., Kraska, M., & Huang, H. (2019). The statistical reasoning learning environment: A comparison of students’ statistical reasoning ability. Journal of Statistics Education, 27(3), 171–187. https://doi.org/10.1080/10691898.2019.1647008
D’Ambrosio, U., & de Campos Almeida, M. (2017). Ethnomathematics and the emergence of mathematics. In J. W. Adams, P. Barmby, & A. Mesoudi (Eds.), The nature and development of mathematics (pp. 69–85). Routledge. https://doi.org/10.4324/9781315648163
Department for Education. (2014). The national curriculum in England: Key stages 3 and 4 framework document. Department for Education of United Kingdom. https://education-uk.org/documents/pdfs/2014-nc-framework-ks3-4.pdf
Ekinci, F., Bektaş, O., Karaca, M., & Yiğit, K. N. (2023). The flipped learning perception scale: A validity and reliability study. Education and Information Technologies, 28(11), 14139–14166. https://doi.org/10.1007/s10639-023-11731-7
Fielding, J., Makar, K., & Ben-Zvi, D. (2025). Developing students’ reasoning with data and data-ing. ZDM – Mathematics Education, 57(1), 1–18. https://doi.org/10.1007/s11858-025-01671-6
Franklin, C., Kader, G., Mewborn, D., Moreno, J., Peck, R., Perry, M., & Scheaffer, R. (2007). Guidelines for assessment and instruction in statistics education (GAISE) report: A pre-k–12 curriculum framework. American Statistical Association. https://www.amstat.org/asa/files/pdfs/gaise/gaiseprek-12_full.pdf
Furuto, L. (2016). Lessons learned: Strengths-based approaches to mathematics education in the Pacific. Journal of Mathematics and Culture, 10(2), 55–72.
Furuto, L. (2018). Knowledge and Action for Change Through Culture, Community and Curriculum. In the 13th International Congress on Mathematical Education (ICME-13 Monographs), Cham (pp. 103–114). https://doi.org/10.1007/978-3-319-72170-5_7
Ganesan, N., & Leong, K. E. (2020). Impact of fathom on statistical reasoning among upper secondary students. Journal of Research in Science, Mathematics and Technology Education, 3(2), 35–50. https://doi.org/10.31756/jrsmte.321
Hasanah, U., Putrawangsa, S., Setiawati, F. A., & Purwanta, E. (2024). Statistical literacy in primary education: An analysis of Indonesian fifth-graders' data interpretation and analysis skills. Journal on Mathematics Education, 15(4), 1335–1356. https://doi.org/10.22342/jme.v15i4.pp1335-1356
Hidetoshi, F., & Rothman, T. (2021). Sacred mathematics: Japanese temple geometry. Princeton University Press. https://press.princeton.edu/books/hardcover/9780691127453/sacred-mathematics
Hjelte, A., Schindler, M., & Nilsson, P. (2020). Kinds of mathematical reasoning addressed in empirical research in mathematics education: A systematic review. Education Sciences, 10(10), 289. https://doi.org/10.3390/educsci10100289
Hu, X., Jiang, Y., & Bi, H. (2022). Measuring science self-efficacy with a focus on the perceived competence dimension: using mixed methods to develop an instrument and explore changes through cross-sectional and longitudinal analyses in high school. International journal of STEM education, 9(1), 47. https://doi.org/10.1186/s40594-022-00363-x
Ilie, S., Forbes, K., Curran, S., & Vermunt, J. D. (2024). Higher education students’ conceptions of learning gain. Active Learning in Higher Education, 1–17. https://doi.org/10.1177/14697874241270461
Jones, G. A., Thornton, C. A., Langrall, C. W., Mooney, E. S., Perry, B., & Putt, I. J. (2000). A framework for characterizing children's statistical thinking. Mathematical thinking and learning, 2(4), 269–307. https://doi.org/10.1207/s15327833mtl0204_3
Kim, H., & Chae, D.-h. (2016). The development and application of a STEAM program based on traditional Korean culture. Eurasia Journal of Mathematics, Science and Technology Education, 12(7), 1925–1936. https://doi.org/10.12973/eurasia.2016.1539a
Kollosche, D. (2021). Styles of reasoning for mathematics education. Educational Studies in Mathematics, 107(3), 471–486. https://doi.org/10.1007/s10649-021-10046-z
Laliyo, L. A. R., Sumintono, B., & Panigoro, C. (2022). Measuring changes in hydrolysis concept of students taught by inquiry model: stacking and racking analysis techniques in rasch model. Heliyon, 8(3), e09126. https://doi.org/10.1016/j.heliyon.2022.e09126
Ling, M.-T., Pang, V., & Ompok, C. C. (2018). Measuring change in early mathematics ability of children who learn using games: Stacked analysis in rasch measurement. In Pacific Rim Objective Measurement Symposium (PROMS) 2016 Conference Proceedings, Singapore (pp. 215–226). https://doi.org/10.1007/978-981-10-8138-5_17
Linn, R. L., & Slinde, J. A. (1977). The determination of the significance of change between pre- and posttesting periods. Review of Educational Research, 47(1), 121–150. https://doi.org/10.3102/00346543047001121
Lipka, J., Hogan, M. P., Webster, J. P., Yanez, E., Adams, B., Clark, S., & Lacy, D. (2005). Math in a cultural context: Two case studies of a successful culturally based math project. Anthropology & Education Quarterly, 36(4), 367–385.
Makar, K. (2013). Young children's explorations of average through informal inferential reasoning. Educational Studies in Mathematics, 86(1), 61–78. https://doi.org/10.1007/s10649-013-9526-y
Makar, K., & Fielding-Wells, J. (2011). Teaching teachers to teach statistical investigations. In Teaching statistics in school mathematics-challenges for teaching and teacher education-New ICMI study series, Dordrecht (pp. 347–358). https://doi.org/10.1007/978-94-007-1131-0_33
Makar, K., & Rubin, A. (2009). A framework for thinking about informal statistical inference. Statistics Education Research Journal, 8(1), 82–105. https://doi.org/10.52041/serj.v8i1.457
Ministry of Education Culture Research and Technology. (2023). Keputusan kepala badan standar, kurikulum, dan asesmen pendidikan kementerian pendidikan, kebudayaan, riset, dan teknologi nomor 008/H/KR/2022 tentang capaian pembelajaran pada pendidikan anak usia dini, jenjang pendidikan dasar, dan jenjang pendidikan menengah pada kurikulum merdeka [Decree of the Head of the Education Standards, Curriculum, and Assessment Agency of the Ministry of Education, Culture, Research, and Technology Number 008/H/KR/2022 concerning learning outcomes in early childhood education, elementary education, and secondary education in the independent curriculum]. Kementerian Pendidikan Kebudayaan Riset dan Teknologi.
Ministry of Education of People’s Republic of China. (2003). Ordinary senior secondary: Mathematics curriculum standards. Ministry of Education of Republic of China.
Ministry of Education Singapore. (2023). Mathematics syllabuses secondary: One to four express course normal (academic) course. Curriculum Planning and Development Division.
Mooney, E. S. (2002). A framework for characterizing middle school students' statistical thinking. Mathematical thinking and learning, 4(1), 23–63. https://doi.org/10.1207/s15327833mtl0401_2
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. The National Council of Teachers of Mathematics, Inc.
Pentecost, T. C., & Barbera, J. (2013). Measuring learning gains in chemical education: A comparison of two methods. Journal of Chemical Education, 90(7), 839–845. https://doi.org/10.1021/ed400018v
Pfannkuch, M. (2006). Informal inferential reasoning. In Working Cooperatively in Statistics Education. Proceedings of the Seventh International Conference on Teaching Statistics. https://www.stat.auckland.ac.nz/~iase/publications/17/6A2_PFAN.pdf
Pfannkuch, M. (2011). The role of context in developing informal statistical inferential reasoning: A classroom study. Mathematical thinking and learning, 13(1-2), 27–46. https://doi.org/10.1080/10986065.2011.538302
Planinic, M., Boone, W. J., Susac, A., & Ivanjek, L. (2019). Rasch analysis in physics education research: Why measurement matters. Physical Review Physics Education Research, 15(2), 020111. https://doi.org/10.1103/PhysRevPhysEducRes.15.020111
Prahmana, R. C. I., Yunianto, W., Rosa, M., & Orey, D. C. (2021). Ethnomathematics: Pranatamangsa system and the birth-death ceremonial in Yogyakarta. Journal on Mathematics Education, 12(1), 93–112. https://doi.org/10.22342/jme.12.1.11745.93-112
Ramadhani, R., Prahmana, R. C. I., Soeharto, S., & Saleh, A. (2024). Integrating traditional food and technology in statistical learning: A learning trajectory. Journal on Mathematics Education, 15(4), 1277–1310. https://doi.org/10.22342/jme.v15i4.pp1277-1310
Ramadhani, R., Saragih, S., Maulida, R., & Simanjuntak, S. M. B. (2022). Measuring changes of students’ statistical reasoning taught by ethnomathematics approach assisted TinkerPlots: A stacking analysis study. JTAM (Jurnal Teori Dan Aplikasi Matematika), 6(3). https://doi.org/10.31764/jtam.v6i3.8375
Ramadhani, R., Saragih, S., & Napitupulu, E. E. (2022). Exploration of students' statistical reasoning ability in the context of ethnomathematics: A study of the rasch model. Mathematics Teaching Research Journal, 14(1), 138–168.
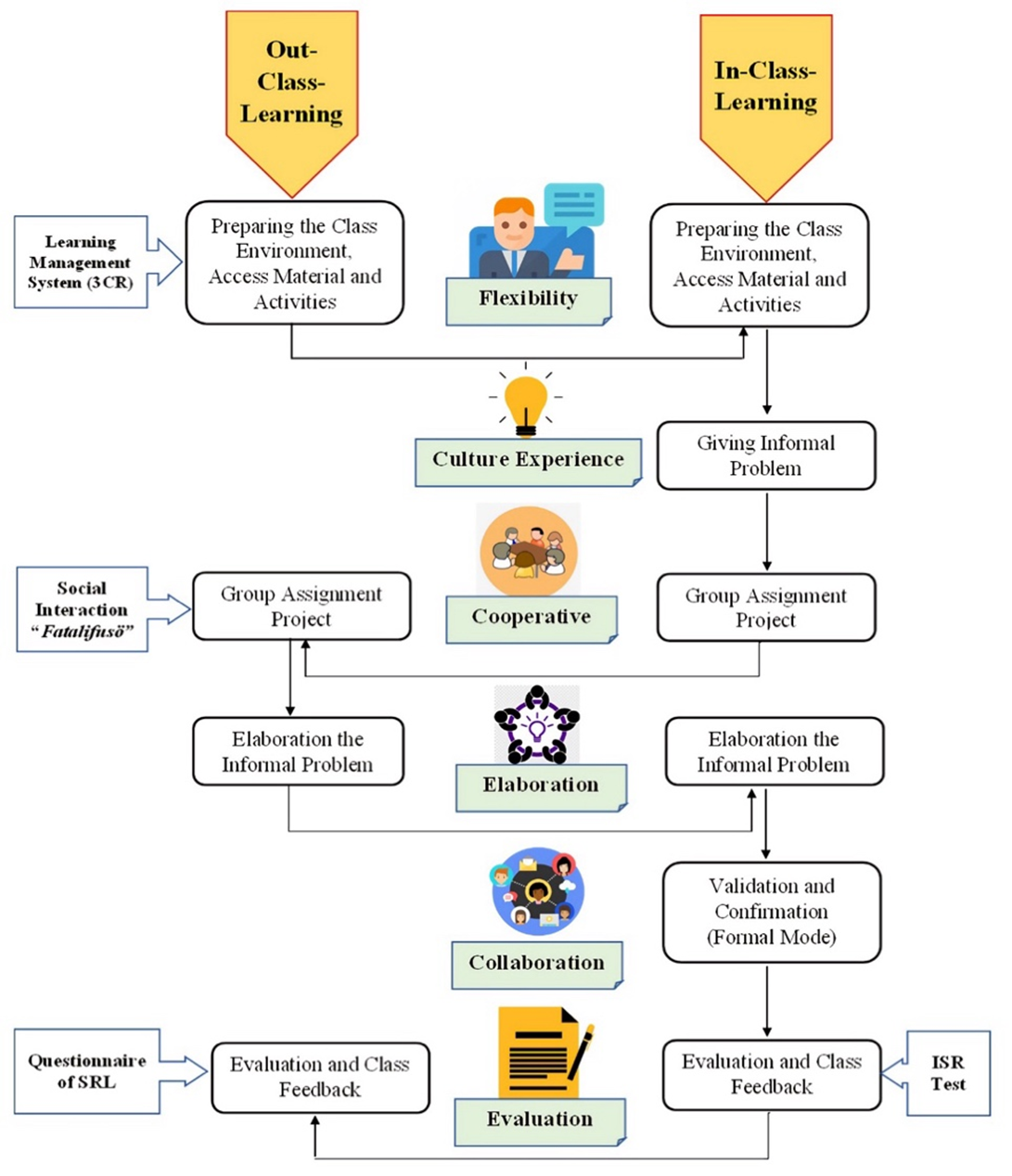
Ramadhani, R., Syahputra, E., & Simamora, E. (2022). Ethno-flipped classroom model: Sebuah rekomendasi model pembelajaran matematika di masa new normal [Ethno-flipped classroom model: A Recommendation for new normal mathematics learning model]. AXIOM : Jurnal Pendidikan dan Matematika, 10(2). https://doi.org/10.30821/axiom.v10i2.10331
Ramadhani, R., Syahputra, E., & Simamora, E. (2023). Ethnomathematics approach integrated flipped classroom model: Culturally contextualized meaningful learning and flexibility. Jurnal Elemen, 9(2), 371–387. https://doi.org/10.29408/jel.v9i2.7871
Ramadhani, R., Syahputra, E., & Simamora, E. (2023). Model ethno–flipped classroom: Solusi pembelajaran fleksibel dan bermakna [Ethno-flipped classroom model: A flexible and meaningful learning solution]. Indonesia Emas Group.
Ramadhani, R., Syahputra, E., & Simamora, E. (2025). Enhancing students' informal statistical reasoning skills through the development of a worksheet rooted in the Nias culture. Mathematics Teaching-Research Journal, 17(2), 104–128.
Rosa, M., & Orey, D. C. (2016). State of the art in ethnomathematics. In Current and future perspectives of ethnomathematics as a program (pp. 11–37). Springer International Publishing. https://doi.org/10.1007/978-3-319-30120-4_3
Sariningsih, R., & Herdiman, I. (2017). Mengembangkan kemampuan penalaran statistik dan berpikir kreatif matematis mahasiswa di Kota Cimahi melalui pendekatan open-ended [Developing statistical reasoning and mathematical creative thinking skills of students in Cimahi City through an open-ended approach]. Jurnal Riset Pendidikan Matematika, 4(2), 239–246. https://doi.org/10.21831/jrpm.v4i2.16685
Schleicher, A. (2023). PISA 2022: Insight and Interpretations. OECD.
Setianingsih, R., & Rahmah, D. A. (2020). Statistical reasoning levels of high school students in solving statistics related problems. Journal of Physics: Conference Series, 1569(4), 042064. https://doi.org/10.1088/1742-6596/1569/4/042064
Smit, R., Dober, H., Hess, K., Bachmann, P., & Birri, T. (2023). Supporting primary students’ mathematical reasoning practice: the effects of formative feedback and the mediating role of self-efficacy. Research in Mathematics Education, 25(3), 277–300. https://doi.org/10.1080/14794802.2022.2062780
Soeharto, S., & Csapó, B. (2022). Assessing Indonesian student inductive reasoning: Rasch analysis. Thinking Skills and Creativity, 46, 101132. https://doi.org/10.1016/j.tsc.2022.101132
Soeharto, S., Martono, M., Hairida, H., Akhmetova, A., Arifiyanti, F., Benő, C., & Charalambos, C. (2024). The metacognitive awareness of reading strategy among pre-service primary teachers and the possibility of rating improvement using Rasch analysis. Studies in Educational Evaluation, 80, 101319. https://doi.org/10.1016/j.stueduc.2023.101319
Sukarelawan, M. I., Jumadi, J., Kuswanto, H., Soeharto, S., & Hikmah, F. N. (2021). Rasch analysis to evaluate the psychometric properties of junior metacognitive awareness inventory in the Indonesian context. Jurnal Pendidikan IPA Indonesia, 10(4), 486–495. https://doi.org/10.15294/jpii.v10i4.27114
Sukoriyanto, S., & Khurin'in, K. (2023). Statistical reasoning of junior high school students in solving central tendency problems mean, median, and modus. AIP Conference Proceedings, 2569(1), 040020. https://doi.org/10.1063/5.0112343
Sumintono, B. (2018). Rasch model measurements as tools in assesment for learning. In 1st International Conference on Education Innovation (ICEI 2017), (pp. 38–42). https://doi.org/10.2991/icei-17.2018.11
Sumintono, B., & Widhiarso, W. (2015). Aplikasi pemodelan rasch pada assessment pendidikan [Application of rasch modeling to educational assessment]. Trim Komunikata.
Sunjaya, D. K., Herawati, D. M. D., Indraswari, N., Megawati, G., & Sumintono, B. (2021). Training and assessing model for the ability of community health volunteers in anthropometric measurement using the rasch stacking and racking analyses. Journal of Environmental and Public Health, 2021, 1–11. https://doi.org/10.1155/2021/5515712
Uzun, Z., & Öğretmen, T. (2021). Test equating with the rasch model to compare pre-test and post-test measurements. Eğitimde ve Psikolojide Ölçme ve Değerlendirme Dergisi, 12(4), 336–347. https://doi.org/10.21031/epod.957614
Valenta, A., Rø, K., & Klock, S. I. (2024). A framework for reasoning in school mathematics: analyzing the development of mathematical claims. Educational Studies in Mathematics, 116(1), 91–111. https://doi.org/10.1007/s10649-024-10309-5
Willoughby, S. D., & Metz, A. (2009). Exploring gender differences with different gain calculations in astronomy and biology. American Journal of Physics, 77(7), 651–657. https://doi.org/10.1119/1.3133087
Wright, B. D. (2003). Rack and stack: time 1 vs. time 2. Rasch measurement transactions, 17(1), 905–906.